久しぶりに方程式というものを書きました。学生って凄いなって思いました。
ということで、今回はまずじゃんけんについて考えます。
じゃんけんは相手がグーを出すときはパーを出すのが最善、パーを出せばチョキを出すのが最善、チョキを出せばグーを出すのが最善・・・とグルグル回って前回の黒龍会と白龍会の例のように、戦略の組み合わせが定まりません。ではじゃんけんにナッシュ均衡はあるのでしょうか?
結論から言うと「お互いがグー、チョキ、パーをそれぞれ1/3の確率で出す」というのがナッシュ均衡となります。これはゲーム理論云々の話の前に直感的にわかることだと思います。※1
前回の黒龍会と白龍会の例のようにお互いが一つの戦略だけを選ぶことを「純戦略」というのに対し、じゃんけんのように複数の戦略を確率的に選ぶことを「混合戦略」と呼びます。混合戦略も含めたナッシュ均衡を求める際はいくつかの戦略をどのような確率で選ぶか、ということがポイントとなります。
ということで前回の黒龍会と白龍会の渋谷横浜の例をもう一度見てみましょう。
| 黒龍会 \ 白龍会 | 渋谷 | 横浜 |
| 渋谷 | (40,20) | (60,45) |
| 横浜 | (45,60) | (30,15) |
図1:再掲 黒龍会と白龍会の利得行列
前回では黒龍会と白龍会は渋谷と横浜のどっちかを選ぶということしかしませんでしたが、今回は確率的に選ぶということをします。
・黒龍会が渋谷をp、横浜を1-pの確率で選択する
・白龍会が渋谷をq、横浜を1-qの確率で選択する
という混合戦略の組み合わせがナッシュ均衡となるようなpとqを求めます。
黒龍会が渋谷を選んだ時の期待利得は
40×q + 60×(1-q) = -20q + 60
黒龍会が横浜を選んだ時の期待利得は
45×q + 30(1-q) = 15q + 30
となります。
黒龍会の最善策が「渋谷に設立する」(p=1)となるのは
-20q + 60 > 15q + 30 のときで、これを解くとq<6/7 黒龍会の最善策が「横浜に設立する」(p=0)となるのは その逆で q>6/7
q=6/7の場合はpをどのような値に取っても黒龍会の期待利得は同じになります。
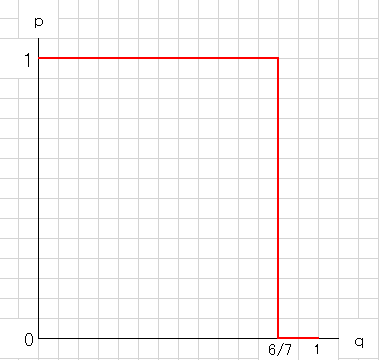
上の関係をpを横軸、qを縦軸とした図に表すと下図のようになります。
図2:黒龍会の最適反応戦略
白龍会についても同様の作業を行います。
白龍会が渋谷を選んだ時の期待利得は
20×p + 60×(1-p) = -40q + 60
白龍会が横浜を選んだ時の期待利得は
45×q + 15(1-q) = 30q + 15
となります。
白龍会の最善策が「渋谷に設立する」(q=1)となるのは
-40q + 60 > 30q + 15 のときで、これを解くとq<9/14 白龍会の最善策が「横浜に設立する」(q=0)となるのは その逆で q>9/14
q=9/14の場合はqをどのような値に取っても白龍会の期待利得は同じになります。
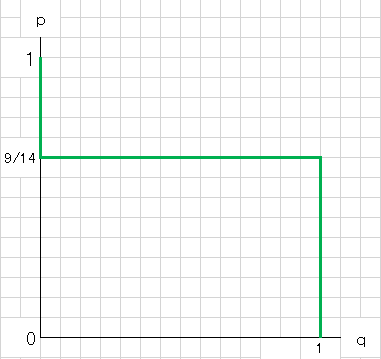
上の関係をpを横軸、qを縦軸とした図に表すと下図のようになります。
図3:白龍会の最適反応戦略
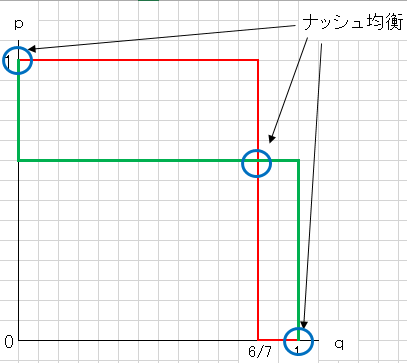
図2と図3を組み合わせてみましょう。
図4:図2と図3を組み合わせてわかるナッシュ均衡
このグラフの交点になるpとqの組み合わせがナッシュ均衡です。つまり
(p,q) = (1,0) , (9/14,6/7) , (0,1)
がこのゲームの解となります。
不人気団体の白龍会の方が渋谷を選択する確率が高いというのは、個人的にはかなり意外でした。ただ黒龍会も9/14の確率で渋谷を選択できそうなので一応は一安心といったところです。
・・・そろそろゲーム理論をバドミントンに応用した話を始めましょう。次回は一つの例として以下のような利得行列で表される例を考えます。
| サーバー \ レシーバー | 前に張る | どちらにも張らない | 後ろに張る |
| ショートサービス | (25,75) | (45,55) | (65,35) |
| ロングサービス | (90,10) | (45,55) | (20,80) |
↑
表の数字は得点期待値で、単位は%です。
次回も今回同様計算が多めになりそうです。読んでて辛かったら遠慮なく仰ってください。よろしくお願いします。
※1 このことの証明は面倒なので割愛しました。ただ、全部を1/3で等確率で出さない戦略には相手により良い戦略を与えてしまう(例えばグーとチョキしか出さない相手にはグーを出し続けるなど)ことから、じゃんけんのナッシュ均衡は上の通りであることが分かると思います。
※参考文献
川越敏司「はじめてのゲーム理論」
渡辺隆裕「ゼミナール ゲーム理論入門」
不人気団体は地方より都心の方が人を集めやすいのかー
意外なような何となくわかるような…、次回いよいよバドミントンの話に期待してます!