いままでのあらすじ：

・ナッシュ均衡とは・・・
「どのプレーヤーも自分の戦略を変更することによってより高い利得を得ることができない戦略の組み合わせ」

・ナッシュ均衡がゲームの解

・複数の戦略を確率的に選ぶことを混合戦略という

・混合戦略のナッシュ均衡を求めるのは数式が沢山でてきて大変

 

難易度的に前回あたりから急激に上がったと思うので、読んでもらえるかどうか心配です。今回は前回の考察から始めようと思います。

サーバー \ レシーバー	前に張る	どちらにも張らない	後ろに張る
ショートサービス	(25,75)	(45,55)	(65,35)
ロングサービス	(90,10)	(45,55)	(20,80)

図1：再掲　サービスの種類とレシーバーの読みの利得行列

この場合のナッシュ均衡は

サーバー　：ショートサービスを5/9～9/13の確率で打つ
レシーバー：どちらにも張らない

となりました。サーバーの確率が約56～69%とブレているのはレシーバーのどちらにも張らない場合の得点期待値を同じにしていることに起因します。

今回の例では非常に簡素な利得行列でバドミントンの深淵には全然迫れていないとは思いますが、以下の3点のことはわかります。

・サーバーはレシーバーに打つコースを読まれないよう散らすのが良い

・レシーバーがサーバーが色んなコースに打つのに対し、バランス良く構えるのが良い

・逆に、相手がどちらかに偏った配球だったり読みをしているならば、徹底して咎めに行くべき

当たり前と言えば当たり前のことかもしれませんが、ゲーム理論によって再確認できました。

 

では次に今回の例の課題を見ていきます。少なくとも自分としては以下の3点が問題だと考えます。

・計算が面倒

・打てるショットの選択肢が少ない

・得点期待値が田口の感覚すぎる

他にも課題はありますが、とりあえずこの3点について調べていきます。

 

まず計算が面倒という点ですが、今回の例は律儀に教科書通りの解き方をしたことに問題がありました。

以下のリンクを参照ください。

https://docs.google.com/spreadsheets/d/1hn98N-ZXiIPBdanW2ISkGsuZiXR7wXgdmFYx9JmKEDI/pubhtml

上のシートではp(ショートサービスの確率)が0.01上がる毎にEr(得点期待値)がどのように変化するかを列挙したものです。

この表をみると0.56~0.69までの間が値が小さくなっているのでナッシュ均衡だな、と見て取ることができます。

一見面倒そうに見えますが、一々計算するよりは遥かに簡単です。また、これを応用しないとこれ以上複雑な問題に中々対応できないんじゃないかと思います。

 

次に、打てるショットの選択肢の問題ですが、一つ増やして選択肢が3×3のパターンを調べてみましょう。

先手 \ 後手	前に走る	ドライブ戦用意	後方警戒
ドライブ	+5	-5	+20
ネット前に落とす	-50	+10	+40
高く上げる	+40	-15	-50

図2：先手からみた得点期待値の利得行列

場面としてはダブルスで互いにサイドバイサイドで正面にドライブか落とすか上げるかの3択、それに対して守る方はどこに意識を置くかという問題を考えます。

この問題のナッシュ均衡の求め方は

ドライブ： 0%, 0%, 0%・・・
落とし　： 0%, 1%, 2%・・・
上げる　：100%, 99%, 98%・・・

という風に先手後手ともに1%ずつ変えて調べます。
久しぶりにプログラムを書きましたが、たかだた100行くらいのプログラムに大苦戦しました。(しかも完成品も問題だらけで研究室でこんなの書いたら怒られるレベル)

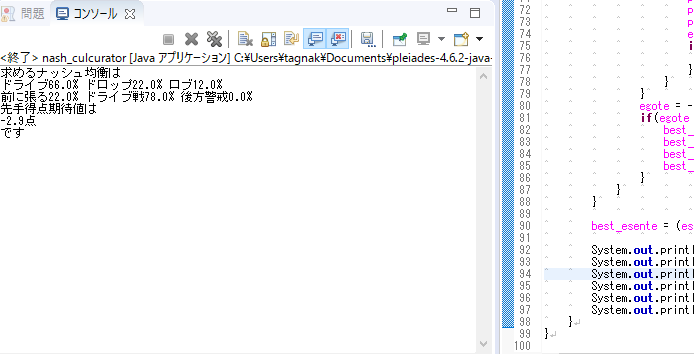
図3：プログラムの結果出力

とはいえ、計算は実行を押せばすぐにしてくれるので、自分自身で計算する煩わしさから解放されたのだけでも良しとします。

先程の利得行列のナッシュ均衡は

先手：ドライブ66%　落とす　22%　上げる　12%
後手：前に走る22%　ドライブ78%　後方警戒 0%

という結果が出ました。※1

プログラミングの出来る人の力と計算数が増えても大丈夫なPCのスペックがあれば、打てるショットの数を増やしてもナッシュ均衡を求めることが出来そうな気はします。

 

最後に正確な得点期待値の求め方の問題です。これが文句なしに最難関だと思います。一番簡単そうなサービス周りの得点期待値を出すのにもひたすら統計取れば良いのか、それとも大量の映像を撮って機械学習させるのか。少なくとも今の自分にはどう考えれば良いのか見当もつかないです。まして、複雑なラリー中の得点期待値なんて求められるようになるのでしょうか。

 

・・・というわけで、ゲーム理論について長々書いてきましたがいかがでしたでしょうか。話の難易度の急激なインフレが起きてしまったような気もしないでもないですが、個人的にはバドミントンの配球に対する新たな発見をいくつか得ることができたので満足しています。

私以上に情熱を持ってゲーム理論×バドミントンの問題を考えてくれる人に出会えたらこの問題についてもう一度真剣に取り組みたいと思いますが、とりあえずここで一旦お終いにします。また別の遊び(?)を見つけたので、それなりの習熟度に達したらこのサイトに記事を投稿するかもしれません。

ご意見ご感想お待ちしております。ではでは。

※参考文献

川越敏司「はじめてのゲーム理論」

渡辺隆裕「ゼミナール　ゲーム理論入門」